Operasi Hitung Bentuk Aljabar
Pada dasarnya operasi hitung pada suku aljabar tidak berbeda dengan operasi hitung pada bilangan bulat. Coba kalian perhatikan contoh-contoh di bawah ini, kemudian kalian ambil kesimpulan sendiri apakah terdapat perbedaan antara operasi hitung suku aljabar dengan operasi hitung bilangan bulat.Pada pembahasan ini kita akan sedikit mengulas tentang bentuk-bentuk operasi hitung pada bentuk aljabar.
1. Operasi Penjumlahan dan Pengurangan Bentuk Aljabar
Operasi hitung penjumlahan dan pengurangan suku aljabar dilakukan dengan cara menjumlahkan atau mengurangkan koefisien antara suku-suku yang sejenis. Perhatikan contoh berikut ini!Tentukan hasil penjumlahan dan pengurangan bentuk aljabar berikut ini!
a. 4x + y – 2x
b. 3a2b – 5ab – 2a2b
Penyelesaian:
a. 4x + y – 2x = 4x – 2x + y
= 2x + y
b. 3a2b – 5ab – 2a2b = 3a2b – 2a2b – 5ab
= a2b – 5ab
Selain dengan cara di atas, penjumlahan dan pengurangan pada suku satu, suku dua, atau suku banyak dapat dihitung dengan cara bersusun ke bawah. Perhatikan contoh berikut ini!
Tentukan hasil penjumlahan dan pengurangan bentuk aljabar berikut ini!
a. 4x + 2x
b. 3a2b + 2ab2– 2a2b + 5ab2
c. 8x – 3x
d. 7ab2 – 3ab – 2ab2 – 8ab
Penyelesaian:
2. Operasi Perkalian dan Pembagian Bentuk Aljabar
Pada bentuk-bentuk aljabar berlaku sifat-sifat penjumlahan dan perkalian seperti pada bilangan bulat. Beberapa sifat tersebut antara lain:- Sifat komutatif penjumlahan, yaitu a + b = b + a
- Sifat asosiatif penjumlahan, yaitu a + (b + c) = (a + b) + c
- Sifat komutatif perkalian, yaitu a × b = b × a
- Sifat asosiatif perkalian, yaitu a × (b × c) = (a × b) × c
- Sifat distributif perkalian terhadap penjumlahan, yaitu: a × (b ± c) = (a × b) ± (a × c)
a. Perkalian Suku Satu dengan Suku Dua atau Suku Banyak
Berikut ini disajikan beberapa contoh perkalian suku satu, baik perkalian dengan suku dua atau dengan suku banyak.Tentukan hasil penjumlahan dan pengurangan bentuk aljabar berikut ini!
a. 4x (x – 2y)
b. 8a (3ab – 2ab2 – 8ab)
Penyelesaian:
Gunakan sifat distributif untuk menyelesaikan permasalahan di atas.
a. 4x (x – 2y) = (4x . x) – (4x (2y))
= 4x2 – 8xy
- = 8a ((3ab – 8ab) – 2ab2)
- = 8a ((-5ab) – 2ab
- = (8a x (-5ab)) – (8a . 2ab2)
- = -40a2b – 16a2b2 (bagi dengan –8)
- = 5a2b + 2a2b2
b. Perkalian Suku Dua dengan Suku Dua
Masih sama dengan perkalian sebelumnya, penyelesaian perkalian suku dua atau binomial tetap menggunakan konsep dasar sifat distributif.Misalkan kita mempunyai suku dua (binomial) yang berbentuk (a + b) dan (c + d). Langkah-langkah penyelesaian yang harus dilakukan adalah seperti terlihat pada gambar berikut.
Jadi (a + b)(c + d) = (ac + bc) + (ad + bd)
Perkalian suku dua dengan suku dua merupakan bentuk perkalian antara suku dua dengan dirinya sendiri atau dapat pula diartikan sebagai pengkuadratan suku dua. Misalkan kita mempunyai suku dua (x+y), maka langkah-langkah penyelesaiannya adalah sebagai berikut.
Coba kalian tentukan langkah-langkah penyelesaian untuk perkalian suku dua yang berbentuk (x-y)2!
Tentukan hasil kali dari (x + 2)2, kemudian sederhanakan!
Penyelesaian:
(x + 2)2 = (x + 2)(x + 2)
= x2 + 2x + 2x + 2 × 2
= x2 + 2(2x) + 4
= x2 + 4x + 4
Jadi (x + 2)2 = x2 + 4x + 4
c. Selisih Dua Kuadrat
Setelah kita mempelajari tentang perkalian suku dua dengan dirinya sendiri (bentuk kuadrat), sekarang kita akan membahas perkalian suku dua antara (x+y) dan (x-y).Langkah-langkah penyelesaiannya sama saja dengan penyelesaian bentuk (x + y)2 dan (x – y)2 yaitu:
Bentuk di atas dikenal dengan istilah selisih dua kuadrat. Agar lebih memahami tentang selisih dua kuadrat, pehatikan contoh berikut ini!
Tentukan hasil kali dari (x – 3)(x + 3)!
Penyelesaian:
(x – 3)(x + 3) = (x – 3)(x + 3)
= (x.x) + (x.3) + ((-3)x) + ((-3)(3))
= x2 + (3x) –3x – 9
= x2 – 9
Jadi (x – 3)(x + 3) = x2 – 9
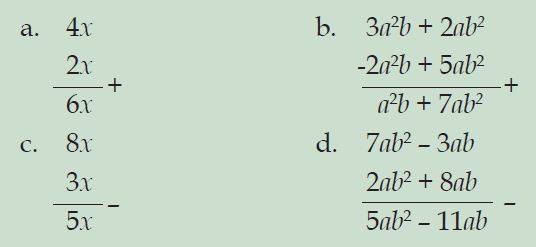
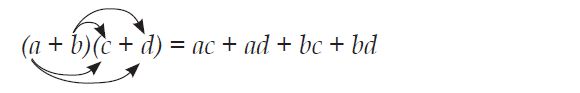
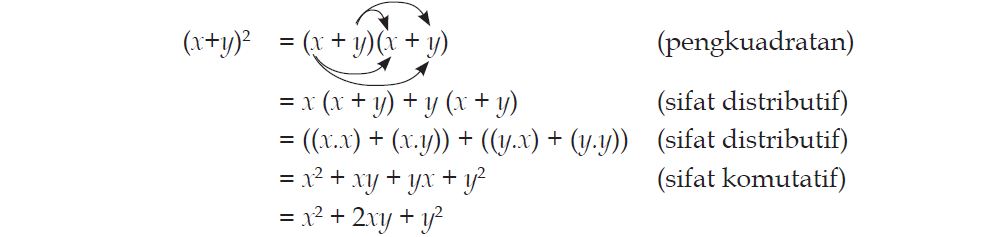
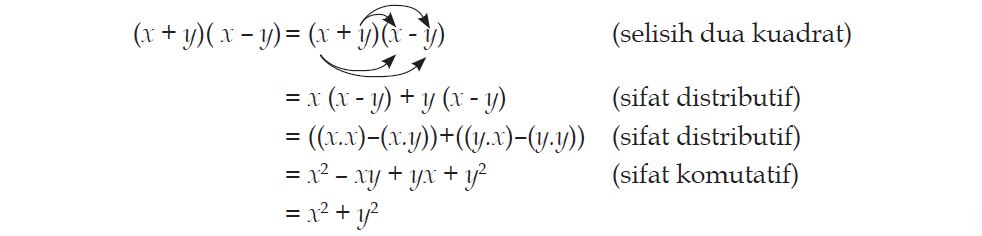
Tidak ada komentar:
Posting Komentar