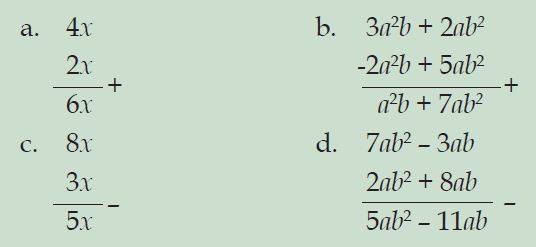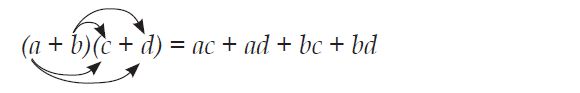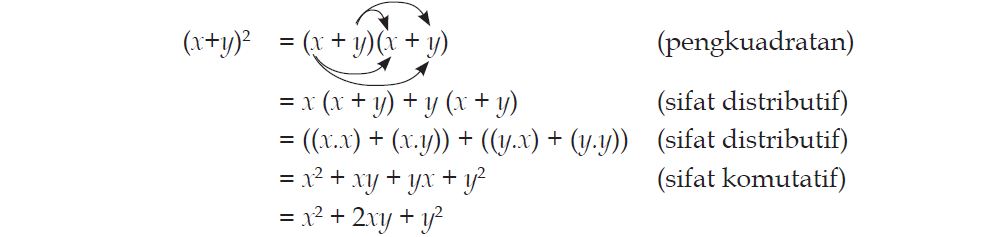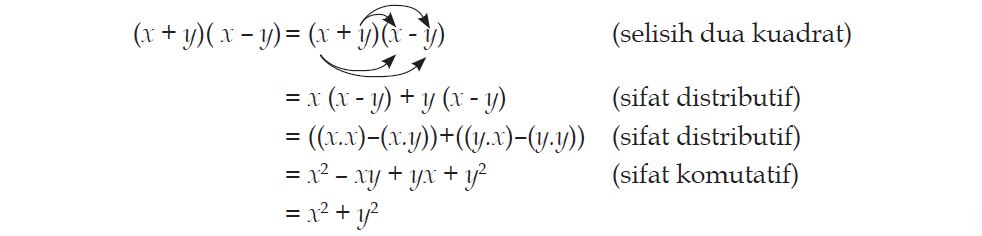jago matematika
blog tentang trik jago matematika
22 Mei 2019
19 Mei 2019
Rasio dua besaran
Banyak masalah dan pengambilan keputusan yang sering kita temui
membutuhkan perbandingan. “Libur telah tiba!” seru Nadia saat liburan
sekolah tiba. Libur kali ini, Nadia dan keluarganya pergi ke Pulau
Merah, Banyuwangi. Di sana, pasir pantai tampak bersih karena tidak ada
sampah. Untuk mengingat saat-saat bahagia, Nadia berfoto bersama
keluarganya. Nadia merasa senang meskipun tidak semua keluarganya mau
difoto karena sedang berteduh di pinggir pantai.
Dari foto di atas, Nadia memperoleh informasi bahwa terdapat 9 laki-laki dan 7 perempuan yang ada di foto. Nadia menceritakan tentang foto tersebut kepada teman-temannya sebagai berikut.
Kita dapat menggunakan perbandingan atau rasio untuk membandingkan besaran suatu benda dengan benda lainnya. Besaran benda yang dimaksud bisa berupa panjang, kecepatan , massa, waktu, banyak benda, dan sebagainya. Perhatikan contoh dan penyelesaiannya berikut.
Siswa di SMP Sukamaju diminta untuk memilih membaca berita melalui media online atau media cetak. Dari 150 siswa, 100 siswa memilih media online dan 50 siswa memilih media cetak. Bagaimana cara kalian membandingkan pilihan siswa membaca melalui online atau media cetak?
Berikut beberapa jawaban dari pertanyaan di atas.
Selama menyelesaikan masalah dalam ini, akan menemukan pernyataan tentang perbandingan dan rasio. Terdapat tiga cara berbeda untuk menyatakan suatu rasio.
Contoh 1 :
Dari 150 siswa diwawancarai tentang kesukaan membaca berita, 100 siswa memilih media online dan 50 siswa memilih media cetak. Rasio banyak siswa yang memilih media online terhadap jumlah siswa yang diwawancarai ditunjukkan sebagai berikut.
Rasio 2 dari 3 menyatakan bahwa 2 dari setiap 3 siswa yang diwawancarai lebih memilih membaca berita melalui media online.
Rasio banyak siswa yang memilih media online terhadap media cetak ditunjukkan sebagai berikut.
Rasio 2 dari 1 menyatakan bahwa untuk setiap 2 siswa yang memilih
membaca berita melalui media online, terdapat 1 siswa yang memilih media
cetak untuk membaca berita.
Contoh 2:
Ita dan Doni adalah teman sekelas. Rumah Ita berjarak sekitar 500 meter dari sekolah. Rumah Doni berjarak sekitar 1,5 km dari sekolah. Berapakah perbandingan jarak rumah Ita dan Doni dari sekolah?
Jarak rumah Ita dari sekolah sekitar 500 meter. Jarak rumah Doni dari sekolah 1,5 km. Perbandingan jarak rumah Ita terhadap jarak rumah Doni dari sekolah adalah
Perbandingan jarak rumah Doni terhadap jarak rumah Ita dari sekolah adalah
atau jarak rumah Doni dari sekolah tiga kali jarak rumah Ita dari sekolah.
Ayo Menalar
1. Bagaimanakah satuan kedua ukuran/kuantitas dalam menyatakan suatu rasio? Satuan kedua ukuran/kuantitas dalam menyatakan suatu rasio haruslah sama.
2. Bagaimanakah pengaruh urutan bilangan-bilangan dalam rasio? Apakah memiliki arti yang berbeda jika dipertukarkan? Jelaskan. Urutan dua bilangan dalam menyatakan suatu rasio sangat penting. Urutan yang berbeda, memiliki arti yang berbeda. Apabila bilangan-bilangan dalam rasio dipertukarkan maka akan memberikan maksud atau penafsiran yang berbeda. Misalkan rasio banyak pembaca media online terhadap pembaca media cetak adalah 2 : 1, maka rasio 1 : 2 memiliki makna yang berbeda. Rasio 1 : 2 bermakna perbandingan banyak pembaca media cetak terhadap pembaca media online.
3. Galuh mendengar dari gurunya bahwa perbandingan laki-laki terhadap perempuan dalam kelasnya tahun ajaran baru ini adalah 5 : 4. Dia bilang, “Apakah perbandingan 5 : 4 ini berarti bahwa hanya ada 5 orang laki-laki di kelas saya?” Bagaimana tanggapan kamu? Bisa jadi benar apa yang pikirkan oleh Galuh apabila memang terdapat 9 orang anak di kelasnya. Namun, perbandingan 5 : 4 merupakan bilangan yang paling sederhana yang menyatakan perbandingan banyaknya siswa laki-laki terhadap banyaknya siswa perempuan. Boleh jadi, banyak siswa laki-laki di kelas adalah 20 dan banyak siswa perempuan di kelasnya adalah 16. Sehingga perbandingan banyak siswa laki-laki terhadap siswa perempuan adalah 20 : 16 atau 5 : 4.
4. Marisa dan Nadia mengikuti Perkemahan Sabtu-Minggu (Persami). Setiap siswa yang mengikuti menyiapkan makanan saat waktu makan tiba. Minggu pagi, Marisa dan Nadia bertugas membuat es jeruk untuk semua peserta Persami. Mereka berdua berniat membuat es jeruk dengan mencampur air putih dan sirup rasa jeruk. Untuk menentukan minuman yang enak, mereka menetapkan beberapa campuran untuk dicoba.
Campuran manakah yang rasa jeruknya sangat kuat?
5. Perkemahan Sabtu-Minggu diselenggarakan di Hutan Lindung Perkemahan. Setiap waktu makan, peserta Persami berkumpul di aula. Di sana terdapat dua jenis meja. Meja yang terbesar mampu menampung sepuluh orang. Sedangkan meja yang lebih kecil menampung delapan orang. Mereka sarapan telur dadar sebagai lauk. Meja yang paling besar disajikan empat telur dadar dan meja yang
lebih kecil disajikan tiga telur dadar.
a. Telur dadar dibagi rata untuk setiap siswa di setiap meja. Apakah siswa yang duduk di meja yang lebih kecil mendapatkan bagian yang sama seperti siswa yang duduk di meja yang lebih besar?
Tidak. Setiap siswa yang duduk di meja besar mendapatkan telur dadar 4/10 bagian sedangkan setiap siswa yang duduk di meja yang lebih kecil mendapatkan telur dadar 3/8 bagian. Oleh karena 4/10 bagian lebih besar dari 3/8 bagian, dapat disimpulkan bahwa siswa yang duduk di meja yang besar mendapatkan bagian yang lebih besar daripada siswa yang duduk di meja yang lebih kecil.
b. Nadia menduga bahwa dia dapat menentukan meja manakah yang setiap siswa memperoleh telur dadar yang lebih besar. Dia menggunakan alasan berikut.
10 – 4 = 6 dan 8 – 3 = 5, jadi setiap siswa yang duduk di meja yang besar memperoleh telur dadar yang besar dibandingkan di meja yang kecil.
Ayo Kita Berlatih
1. Kalian dapat menjelaskan ukuran sebuah pohon dengan membandingkannya terhadap pohon lain atau benda yang lain.
Tabel Pohon-Pohon Bernilai Ekonomis di Indonesia
Gunakan tabel di atas untuk menjawab pertanyaan berikut.
2. Manusia yang penah hidup di Indonesia dengan ukuran badan tertinggi adalah Suparwono. Dia adalah mantan atlet basket. Tinggi badan Suparwono adalah sekitar 2,4 meter. Tuliskan dua pernyataan untuk membandingkan tinggi Suparwono terhadap tinggi kelima pohon. Gunakan pecahan, perbandingan, persentase, atau selisih.
3. Dalam tes menguji rasa dua jenis susu kotak, 780 siswa memilih Fullcream. Hanya 220 siswa yang memilih Hi-Cal. Lengkapi setiap pernyataan berikut.
4. Kelas VIID di SMP Mandala mengumpulkan data berbagai jenis film yang disukai oleh siswa kelas VII dan VIII. Jenis film yang dipilih siswa SMP Mandala
Lengkapi pernyataan berikut berdasarkan tabel di atas.
5. Bagaimana cara kalian membandingkan waktu yang dihabiskan Iqbal dalam berbagai aktivitas selama liburan? Jelaskan.
Cara yang digunakan untuk membandingkan waktu yang dihabiskan Iqbal
selama liburan adalah dengan membandingkan waktu (jam) yang digunakan
untuk setiap kegiatan dengan 48 jam.
6. Tentukan apakah pernyataan-pernyataan berikut sesuai dengan tabel yang dibuat Iqbal dalam menghabiskan waktunya selama liburan.
7. Pilihan Ganda. Manakah diantara pernyataan berikut yang benar atas pernyataan “Laki-laki lebih banyak dari wanita dengan rasio 9 terhadap 5.”
a. Laki-laki empat lebih banyak daripada wanita.
b. Banyak laki-laki adalah 1,8 kali banyak wanita.(benar)
c. Banyak laki-laki dibagi banyak wanita sama dengan hasil dari 5÷9.
d. Lima dari sembilan orang adalah wanita.
8. Di perkemahan, Mario mampu membuat 3 anyaman bambu dalam 2 jam. Dani mampu membuat anyaman bambu dalam 3 jam.
9. Tentukan nilai yang belum diketahui supaya setiap pernyataan berikut benar.
10. Misalkan seorang reporter melaporkan, “90% dari penonton di Stadion Diponegoro berusia antara 25 dan 55.” Adinda mengira bahwa hal ini berarti hanya 100 orang di dalam stadion, dan 90 orang dari mereka berusia antara 22 dan 55. Apakah kalian setuju dengan Adinda? Jika tidak, apa maksud dari pernyataan reporter?
Tidak setuju dengan Adinda. Maksud dari reporter 90% dari penonton di stadion berusia antara 25 dan 55 adalah banyaknya reporter yang berusia antara 25 dan 55 dengan jumlah semua penonton dalam stadion adalah 90 : 100 atau 9 : 10.
Dari foto di atas, Nadia memperoleh informasi bahwa terdapat 9 laki-laki dan 7 perempuan yang ada di foto. Nadia menceritakan tentang foto tersebut kepada teman-temannya sebagai berikut.
- Tujuh dari enam belas orang yang ada di foto adalah perempuan.
- Perbandingan banyak laki-laki dan perempuan di foto adalah 9 berbanding 7.
- Banyak laki-laki di dalam foto adalah dua lebih banyak daripada perempuan.
Kita dapat menggunakan perbandingan atau rasio untuk membandingkan besaran suatu benda dengan benda lainnya. Besaran benda yang dimaksud bisa berupa panjang, kecepatan , massa, waktu, banyak benda, dan sebagainya. Perhatikan contoh dan penyelesaiannya berikut.
Siswa di SMP Sukamaju diminta untuk memilih membaca berita melalui media online atau media cetak. Dari 150 siswa, 100 siswa memilih media online dan 50 siswa memilih media cetak. Bagaimana cara kalian membandingkan pilihan siswa membaca melalui online atau media cetak?
Berikut beberapa jawaban dari pertanyaan di atas.
- 1/3 dari siswa SMP Sukamaju yang mengikuti survei memilih media cetak untuk membaca berita.
- Rasio banyak siswa yang memilih media online terhadap media cetak adalah 2 : 1.
- 1 dari 3 siswa memilih media cetak.
- Banyak siswa yang memilih membaca online adalah 50 lebih banyak dari siswa yang membaca berita melalui media cetak.
- Banyak siswa yang membaca online dua kali lipat dari siswa yang membaca melalui media cetak.
Selama menyelesaikan masalah dalam ini, akan menemukan pernyataan tentang perbandingan dan rasio. Terdapat tiga cara berbeda untuk menyatakan suatu rasio.
- Pecahan, misalnya 2/3
- Dua bilangan yang dipisahkan oleh titik dua ( : ), misalnya 2 : 3.
- Dua bilangan yang dipisahkan oleh kata dari, misalnya 2 dari 3.
Contoh 1 :
Dari 150 siswa diwawancarai tentang kesukaan membaca berita, 100 siswa memilih media online dan 50 siswa memilih media cetak. Rasio banyak siswa yang memilih media online terhadap jumlah siswa yang diwawancarai ditunjukkan sebagai berikut.
| 100 | = | 2 | atau 2 : 3 atau 2 banding 3 |
| 150 | 3 |
Rasio banyak siswa yang memilih media online terhadap media cetak ditunjukkan sebagai berikut.
| 100 | = | 2 | atau 2 : 1 atau 2 banding 1 |
| 50 | 1 |
Contoh 2:
Ita dan Doni adalah teman sekelas. Rumah Ita berjarak sekitar 500 meter dari sekolah. Rumah Doni berjarak sekitar 1,5 km dari sekolah. Berapakah perbandingan jarak rumah Ita dan Doni dari sekolah?
Jarak rumah Ita dari sekolah sekitar 500 meter. Jarak rumah Doni dari sekolah 1,5 km. Perbandingan jarak rumah Ita terhadap jarak rumah Doni dari sekolah adalah
| 500 : 1.500 = 1 : 3, atau | 1 |
| 3 |
| 1. 500 : 500 = 3 : 1, atau | 3 |
| 1 |
Ayo Menalar
1. Bagaimanakah satuan kedua ukuran/kuantitas dalam menyatakan suatu rasio? Satuan kedua ukuran/kuantitas dalam menyatakan suatu rasio haruslah sama.
2. Bagaimanakah pengaruh urutan bilangan-bilangan dalam rasio? Apakah memiliki arti yang berbeda jika dipertukarkan? Jelaskan. Urutan dua bilangan dalam menyatakan suatu rasio sangat penting. Urutan yang berbeda, memiliki arti yang berbeda. Apabila bilangan-bilangan dalam rasio dipertukarkan maka akan memberikan maksud atau penafsiran yang berbeda. Misalkan rasio banyak pembaca media online terhadap pembaca media cetak adalah 2 : 1, maka rasio 1 : 2 memiliki makna yang berbeda. Rasio 1 : 2 bermakna perbandingan banyak pembaca media cetak terhadap pembaca media online.
3. Galuh mendengar dari gurunya bahwa perbandingan laki-laki terhadap perempuan dalam kelasnya tahun ajaran baru ini adalah 5 : 4. Dia bilang, “Apakah perbandingan 5 : 4 ini berarti bahwa hanya ada 5 orang laki-laki di kelas saya?” Bagaimana tanggapan kamu? Bisa jadi benar apa yang pikirkan oleh Galuh apabila memang terdapat 9 orang anak di kelasnya. Namun, perbandingan 5 : 4 merupakan bilangan yang paling sederhana yang menyatakan perbandingan banyaknya siswa laki-laki terhadap banyaknya siswa perempuan. Boleh jadi, banyak siswa laki-laki di kelas adalah 20 dan banyak siswa perempuan di kelasnya adalah 16. Sehingga perbandingan banyak siswa laki-laki terhadap siswa perempuan adalah 20 : 16 atau 5 : 4.
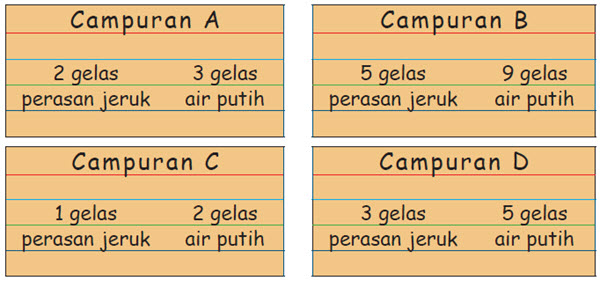
4. Marisa dan Nadia mengikuti Perkemahan Sabtu-Minggu (Persami). Setiap siswa yang mengikuti menyiapkan makanan saat waktu makan tiba. Minggu pagi, Marisa dan Nadia bertugas membuat es jeruk untuk semua peserta Persami. Mereka berdua berniat membuat es jeruk dengan mencampur air putih dan sirup rasa jeruk. Untuk menentukan minuman yang enak, mereka menetapkan beberapa campuran untuk dicoba.
Campuran manakah yang rasa jeruknya sangat kuat?
| No | Campuran | Uraian | |||
|---|---|---|---|---|---|
| 1. | Campuran A | Campuran A terdiri dari 2 gelas sirup dan 3 gelas air putih, berarti persentase kadar sirup dalam minuman adalah
| |||
| 2. | Campuran B | Campuran B terdiri dari 5 gelas sirup dan 9 gelas air putih, berarti persentase kadar sirup dalam minuman adalah
| |||
| 3. | Campuran C | Campuran C terdiri dari 1 gelas sirup dan 2 gelas air putih, berarti persentase kadar sirup dalam minuman adalah
| |||
| 4. | Campuran D | Campuran D terdiri dari 3 gelas sirup dan 5 gelas air putih, berarti persentase kadar sirup dalam minuman adalah
| |||
| 5. | Kesimpulan | Berdasarkan persentase di atas, dapat dilihat bahwa campuran A memiliki rasa yang lebih kuat. |
5. Perkemahan Sabtu-Minggu diselenggarakan di Hutan Lindung Perkemahan. Setiap waktu makan, peserta Persami berkumpul di aula. Di sana terdapat dua jenis meja. Meja yang terbesar mampu menampung sepuluh orang. Sedangkan meja yang lebih kecil menampung delapan orang. Mereka sarapan telur dadar sebagai lauk. Meja yang paling besar disajikan empat telur dadar dan meja yang
lebih kecil disajikan tiga telur dadar.
a. Telur dadar dibagi rata untuk setiap siswa di setiap meja. Apakah siswa yang duduk di meja yang lebih kecil mendapatkan bagian yang sama seperti siswa yang duduk di meja yang lebih besar?
Tidak. Setiap siswa yang duduk di meja besar mendapatkan telur dadar 4/10 bagian sedangkan setiap siswa yang duduk di meja yang lebih kecil mendapatkan telur dadar 3/8 bagian. Oleh karena 4/10 bagian lebih besar dari 3/8 bagian, dapat disimpulkan bahwa siswa yang duduk di meja yang besar mendapatkan bagian yang lebih besar daripada siswa yang duduk di meja yang lebih kecil.
b. Nadia menduga bahwa dia dapat menentukan meja manakah yang setiap siswa memperoleh telur dadar yang lebih besar. Dia menggunakan alasan berikut.
10 – 4 = 6 dan 8 – 3 = 5, jadi setiap siswa yang duduk di meja yang besar memperoleh telur dadar yang besar dibandingkan di meja yang kecil.
- Apa arti 6 dan 5 yang dimaksud dalam alasan Nadia? 6 dan 5 yang dimaksud Nadia adalah selisih banyak anak dengan banyak telur dadar yang tersedia.
- Apakah kalian setuju dengan alasan Nadia? Tidak setuju.
- Seandainya disediakan sembilan telur dadar di meja besar. Apakah alasan yang digunakan Nadia menjadi benar? Tidak. Jika disediakan 9 telur dadar di meja besar, maka selisih banyak siswa dan telur dadar menjadi 1. Sehingga alasan yang digunakan Nadia menjadi kurang tepat untuk menentukan meja mana yang setiap siswa memperoleh telur dadar yang lebih besar.
Ayo Kita Berlatih
1. Kalian dapat menjelaskan ukuran sebuah pohon dengan membandingkannya terhadap pohon lain atau benda yang lain.
Tabel Pohon-Pohon Bernilai Ekonomis di Indonesia
| Nama Pohon dan Asal | Tingkat Kepunahan | Tinggi (meter) | Diameter (cm) |
|---|---|---|---|
| Damar (Maluku) | Rentan | 65 | 150 |
| Ulin/Kayu Besi (Kalimantan) | Rentan | 50 | 120 |
| Kayu Hitam Sulawesi (Sulawesi) | Rentan | 40 | 100 |
| Gaharu (Kalimantan) | Rentan | 40 | 60 |
| Ramin (Kalimantan) | Rentan | 40 | 20 |
- Anton mengatakan bahwa rasio diameter Ramin terhadap diameter Ulin adalah 1 : 6. Apakah pernyataan Anton benar? Jelaskan. Benar. Perbandingan diameter Ramin terhadap Ulin adalah 20 : 120 atau 1: 6.
- Ria mengatakan bahwa selisih tinggi Damar dan Gaharu adalah 25. Apakah benar? Jelaskan.65-40 = 25.
- Leni mengatakan bahwa keliling Ulin sekitar tiga perempat kali keliling Damar. Apakah benar? Jelaskan. Benar. Keliling Ulin = π × d = 120π. Keliling Damar = π × d = 150π. Perbandingan keliling Ulin terhadap damar adalah = 120π : 150π, atau 120/150 = 3/4 . Jadi, benar bahwa keliling ulin sama dengan tiga perempat dari keliling damar.
2. Manusia yang penah hidup di Indonesia dengan ukuran badan tertinggi adalah Suparwono. Dia adalah mantan atlet basket. Tinggi badan Suparwono adalah sekitar 2,4 meter. Tuliskan dua pernyataan untuk membandingkan tinggi Suparwono terhadap tinggi kelima pohon. Gunakan pecahan, perbandingan, persentase, atau selisih.
- Perbandingan tinggi badan Suparwono dengan tinggi kayu hitam adalah 3 : 5 (240 : 400).
- Selisih tinggi badan Suparwono dengan diameter kayu damar adalah 90 cm (240-150).
- Nilai pecahan diameter kayu ramin terhadap tinggi badan Suparwono adalah 1/12 (20/240)
3. Dalam tes menguji rasa dua jenis susu kotak, 780 siswa memilih Fullcream. Hanya 220 siswa yang memilih Hi-Cal. Lengkapi setiap pernyataan berikut.
- Terdapat 560 siswa lebih banyak yang memilih Fullcream.(780 - 220 = 560)
- Siswa yang memilih Fulcream lebih banyak daripada yang memilih Hi-Cal dengan rasio 28 : 11 (560 : 220)
4. Kelas VIID di SMP Mandala mengumpulkan data berbagai jenis film yang disukai oleh siswa kelas VII dan VIII. Jenis film yang dipilih siswa SMP Mandala
| Jenis Film | Siswa Kelas VII | Siswa Kelas VIII |
|---|---|---|
| Action | 75 | 80 |
| Drama | 105 | 150 |
| Total | 180 | 240 |
- Perbandingan banyak siswa kelas VII yang memilih film drama terhadap banyak siswa kelas VIII yang memilih drama adalah 7 banding 10 (105 :150)
- Pecahan yang menyatakan jumlah seluruh siwa (kelas VII dan kelas VIII) yang memilih film action adalah kelas VII = 5/12 (75/180) dan kelas VII = 1/3 (80/240)
- Perbandingan banyak siswa (kelas VII dan kelas VIII) yang memilih film drama terhadap banyak siswa (kelas VII dan kelas VIII) yang memilih film action adalah 51:31 (255:155)
5. Bagaimana cara kalian membandingkan waktu yang dihabiskan Iqbal dalam berbagai aktivitas selama liburan? Jelaskan.
| Aktivitas | Waktu (jam) |
|---|---|
| Tidur | 18 |
| Makan | 2,5 |
| Rekreasi | 8 |
| Menonton TV | 6 |
| Mengerjakan PR atau Soal Latihan | 2 |
| Bermain ke rumah teman | 2 |
| Lainnya | 9,5 |
| Jumlah | 48 |
6. Tentukan apakah pernyataan-pernyataan berikut sesuai dengan tabel yang dibuat Iqbal dalam menghabiskan waktunya selama liburan.
- Iqbal menghabiskan seperenam waktunya untuk menonton TV.(benar)(6/48)
- Rasio lama menonton TV terhadap lama mengerjakan PR atau Soal Latihan adalah 3 : 1.(benar)(6:2=3:1)
- Rekreasi, Bermain ke rumah teman, dan menonton TV menghabiskan sekitar sepertiga dari waktu liburannya.(benar)(16/48=1/3)
- Lama Iqbal mengerjakan PR atau soal latihan hanya seperlima dari lama dia menonton TV.(salah)(seharusnya 2/6 =1/3)
- Tidur, makan, dan aktivitas lainnya menghabiskan waktu 12 jam lebih banyak dari total semua aktivitasnya.(salah)(seharusnya 48-30 =18)
7. Pilihan Ganda. Manakah diantara pernyataan berikut yang benar atas pernyataan “Laki-laki lebih banyak dari wanita dengan rasio 9 terhadap 5.”
a. Laki-laki empat lebih banyak daripada wanita.
b. Banyak laki-laki adalah 1,8 kali banyak wanita.(benar)
c. Banyak laki-laki dibagi banyak wanita sama dengan hasil dari 5÷9.
d. Lima dari sembilan orang adalah wanita.
8. Di perkemahan, Mario mampu membuat 3 anyaman bambu dalam 2 jam. Dani mampu membuat anyaman bambu dalam 3 jam.
- Siapakah yang membuat anyaman lebih cepat, Mario atau Dani?(Mario membuat anyaman lebih cepat daripada Dani)
- Berapa lama waktu yang dibutuhkan Mario untuk membuat 12 anyaman?(8 jam)
- Berapa lama waktu yang dibutuhkan Dani untuk membuat 12 anyaman?(9 jam)
9. Tentukan nilai yang belum diketahui supaya setiap pernyataan berikut benar.
10. Misalkan seorang reporter melaporkan, “90% dari penonton di Stadion Diponegoro berusia antara 25 dan 55.” Adinda mengira bahwa hal ini berarti hanya 100 orang di dalam stadion, dan 90 orang dari mereka berusia antara 22 dan 55. Apakah kalian setuju dengan Adinda? Jika tidak, apa maksud dari pernyataan reporter?
Tidak setuju dengan Adinda. Maksud dari reporter 90% dari penonton di stadion berusia antara 25 dan 55 adalah banyaknya reporter yang berusia antara 25 dan 55 dengan jumlah semua penonton dalam stadion adalah 90 : 100 atau 9 : 10.
POLA BILANGAN
Memahami Macam – Macam Pola Bilangan Dalam Matematika
Macam – macam pola bilangan | Pola bilangan merupakan sub bab dari materi barisan bilangan atau bab yang perlu di fahami terlebih dahulu sebelum melanjut pada materi barisan aritmatika dan barisan geometri .Pola bilangan juga merupakan materi yang tidak kalah penting untuk dipelajari .
Pola bilangan sendiri memiliki arti suatu susunan bilangan yang memiliki bentuk teratur atau suatu bilangan yang tersusun dari beberapa bilangan lain yang membentuk suatu pola . Dan pola bilanga juga memiliki banyak jenisnya atau macamnya . Pada kesempatan kali ini , kita akan mempelajarinya bersama .
Macam – macam Pola Bilangan
Macam – macam pola bilngan meliputi beberapa jenis berikut ini :
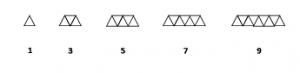
- Pola Bilangan Ganjil
Poal
bilangan ganjil yaitu pola bilangan yang terbentuk dari bilangan –
bilangan ganjil . Sedangkan pengertian dari bilangan ganjil sendiri
memiliki arti suatu bilangan asli yang tidak habis dibagi dua ataupun
kelipatannya .
- pola bilangan ganjil adalah : 1 , 3 , 5 , 7 , 9 , . . . .
- Gambar Pola bilangan ganjil :
- Rumus Pola Bilangan ganjil
1 , 3 , 5 , 7 , . . . , n , maka rumus pola bilangan ganjil ke n adalah :
Un = 2n – 1
Contoh :
1 , 3 , 5 , 7 , . . . , ke 10
Berapakah pola bilangan ganjil ke 10 ?
Jawab :
Un = 2n – 1
U10 = 2 . 10 – 1
= 20 – 1 = 19
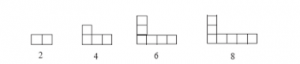
2. Pola Bilangan Genap
pola
bilangan genap yaitu pola bilangan yang terbentuk dari bilangan –
bilangan genap . Bilangan genap yaitu bilangan asli yaitu bilangan asli
yang habis dibagi dua atau kelipatannya .
- Pola bilangan genap adalah : 2 , 4 , 6 , 8 , . . .
- Gambar pola bilangan genap :
- Rumus Pola bilangan genap
2 , 4 , 6 , 8 , . . . . , n maka rumus pola bilangan genap ke n adalah :
Un = 2n
Contoh :
2 , 4 , 6 , 8 , . . . ke 10 .berapakah pola bilangan genap ke 10 ?
jawab :
Un = 2n
U10 = 2 x 10
= 20
3. Pola bilangan Persegi
Pola bilangan persegi , yaitu suatu barisan bilangan yang membentuk suatu pola persegi .
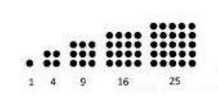
- Pola bilangan persegi adalah 1 , 4 , 9 , 16 , 25 , . . .
- Gambar Pola bilangan persegi :
- Rumus Pola bilangan persegi
1 , 4 , 9 , 16 , 25 , 36 , . . . , n maka rumus untuk mencari pola bilangan persegi ke n adalah :
Un = n2
Contoh :
Dari
suatu barisan bilangan 1 , 2 , 9 , 16 , 25 , 36 , . . . ,ke 10 .
Berapakah pola bilangan ke 10 dalam pola bilangan persegi ?
Jawab :
Un = n2
U10 = 102 = 100
4. Pola Bilangan Persegi Panjang
Pola bilangan persegi panjang yaitu suatu barisan bilangan yang membentuk pola persegi panjang .
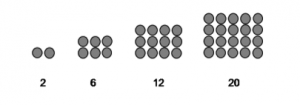
- Pola persegi panjang adalah 2 , 6 , 12 , 20 , 30 , . . .
- Gambar Pola Bilangan persegi panjang :
- Rumus pola bilangan persegi panjang
2 , 6 , 12 , 20 , 30 , . . . n , maka Rumus Pola bilangan Persegi panjang ke n adalah :
Un = n . n + 1
Contoh :
Dari suatu barisan bilangan 2 , 6 , 12 , 20 , 30 , . . . , ke 10 . Berapakah pola bilangan persegi ke 10 ?
Jawab :
Un = n . n+ 1
U10 = 10 . 10 + 1
= 10 . 11
= 110
5. Pola Bilangan Segitiga
Pola bilangan segitiga yaitu suatu barisan bilangan yang membentuk sebuah pola bilangan segitiga .
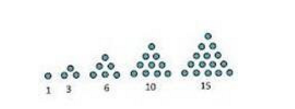
- Pola bilangan segitiga adalah : 1 , 3 , 6 , 10 , 15 , . . .
- Gambar Pola bilangan segitiga :
- Rumus Pola Bilangan Segitiga :
1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , ke n . Maka rumus pola bilangan segitiga ke n adalah :
Un = 1 / 2 n ( n + 1 )
Contoh Soal :
Dari suatu barisan bilangan 1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , ke 10 . Berapakah pola bilangan segitiga ke 10 ?
Jawab :
Un = 1/2 n ( n + 1 )
U 10 = 1/2 .10 ( 10 + 1 )
= 5 ( 11 ) = 55
6. Pola Bilangan FIBONACCI
Pola bilangan fibonacci yaitu suatu bilangan yang setiap sukunya merupakan jumlah dari dua suku di depanya .
- Pola bilangan fibonacci :
1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 56 , . . .
2 , 2 , 4 , 6 , 10 , 16 , 26 , 42 , . . ..
Demikian penjelasan mengenai pola bilangan dalam ilmu matematika .
Pada dasarnya , pola bilangan merupakan suatu bentuk barisan bilangan .
Apabila kita dalam memperhatikanya tidak terlalu cermat, maka pola yang
satu dengan pola bilangan yang lain tidak ada bedanya . Namun , pola
bilangan memiliki fungsi yang sangat besar yaitu supaya lebih mudah
dalam mengerjakan barisan aritmatika dan geometri . Semoga bermanfaat . .
.
BARISAN ARITMATIKA
Pengertian, Contoh dan Rumus Barisan Aritmatika beserta Contoh Soal Barisan Aritmatika
Barisan aritmatika – berdasarkan pola, barisan bilangan dapat dibagi kedalam 2 bagian, yakni barisan arimetika (atau yang disebut dengan barisan hitung) dengan barisan geometri atau disebut dengan (barisan ukur). Untuk lebih jelasnya tentang barisan aritmatika, simak ulasan dibawah ini. Pengertian barisan aritmetika ialah barisan bilangan yang memiliki beda ataupun selisih yang tetap diantara 2 suku barisan dan berurutan.Diketahui sebuah barisan bilangan dengan urutan dibawah ini:
Pada barisan bilangan diatas mempunyai beda ataupun selisih 3 diantara 2 suku barisan berurutan. Jadi, barisan bilangan tersebut termasuk barisan aritmetika.
Selanjutnya diketahui barisan bilangan dengan urutan:
Pada barisan bilangan tersebut mempunyai beda atau selisih tetap diantara 2 suku barisan berurutan, yakni –4. Jadi, barisan bilangan tersebut adalah barisan aritmetika.
Bila b bernilai positif, barisan aritmetika tersebut dikatakan sebagai barisan aritmetika naik. Dan sebaliknya, bila b nilainya negatif, itu berarti barisan aritmetika tersebut disebut dengan barisan arimetika turun.
Lebih jelasnya, silahkan perhatikan contoh soal dibawah ini.
Contoh Soal Pada Barisan Aritmatika
Tentukanlah jenis barisan aritmetika dibawah ini berdasarkan dengan nilai bedanya.- 30, 32, 34, 36, 38, 40, 42, 44, 46, …
- 18, 15, 12, 9, 6, 3, 0, -3, -6, -9, …
- −10, −14, –18, −22, −26, -30, -34, -38, …
Rumus Barisan Aritmatika
Setelah kamu memahami tentang barisan aritmatika naik turun, kini saatnya untuk mempelajari rumus barisan aritmatika. Cara mencari salah satu dari suku barisan bila yang diketahui cuma suku pertama dengan bedanya saja bisa kamu gunakan rumus barisan aritmatika.Bagaimanakah cara mencari beda bila yang diketahui cuma suku pertama dengan satu suku barisan lainnya? Untuk menjawabnya, langsung pelajari uraian yang ada berikut ini.
Diketahui ada barisan bilangan aritmetika dibawah ini.
U1, U2, U3, U4, U5, U6, …, Un – 1 , Un
Dengan melihat barisan diatas, dapat diperoleh kesimpulan:
U1 = a (untuk suku pertama yang dilambangkan oleh a)
U2 = U1 + b = a + b
U3 = U2 + b = (a + b) + b = a + 2b
U4 = U3 + b = (a + 2b) + b = a + 3b
U5 = U4 + b = (a + 3b) + b = a + 4b
U6 = U5 + b = (a + 4b) + b = a + 5b
…
Un = Un − 1 + b = (a + (n − 2) b ) + b = a + (n − 1) b
Sehingga rumus ke-n pada barisan aritmetika diatas bisa ditulis sebagai berikut ini.

Sedangkan untuk mencari beda di suatu barisan aritmetika, kamu bisa perhatikan uraian berikut ini.
U2 = U1 + b jadi, b = U2 − U1
U3 = U2 + b jadi, b = U3 − U2
U4 = U3 + b jadi, b = U4 − U3
U5 = U4 + b jadi, b = U5 − U4
…
Un = Un − 1 + b jadi, b = Un − Un − 1
Sehingga beda dari barisan aritmetika dapat dinyatakan sebagai berikut ini.

Itulah pembahasan tentang barisan aritmetika. Selamat belajar.
BENTUK ALJABAR
Hayo, siapa di antara kamu yang masih ingat apa itu aljabar? Aljabar
merupakan salah satu dari cabang Matematika yang mempelajari tentang
penyelesaian masalah dengan menggunakan huruf-huruf untuk mewakili
angka-angka. Bentuk aljabar ini terdiri dari variabel (nilai
berubah), konstanta (nilai tetap), dan koefisien (faktor pengali).
Misalnya 2a + 1 nih, Squad. Berarti, 2 merupakan koefisiennya, a
merupakan variabelnya, dan 1 merupakan konstantanya. Bagaimana, sampai
di sini kamu sudah ingat?
Oke, kalau begitu, selanjutnya mari kita masuk ke operasi perpangkatan pada aljabar, ya. Kira-kira, bagaimana sih cara untuk menyelesaikan operasi perpangkatan pada aljabar? Yuk, langsung saja kita simak pada artikel di bawah ini. Let’s scroll it, Squad!
Sebelumnya, ayo kita simak kisah Rogu berikut ini dan kita selesaikan bersama-sama, ya!
Pada
saat upacara bendera di sekolah, Rogu bergabung ke dalam grup paduan
suara yang selama ini ia idam-idamkan. Grup tersebut terdiri dari 5
baris. Baris pertama, bertugas untuk memainkan pianika, baris kedua
bertugas untuk memainkan recorder, dan baris ketiga sampai
kelima bertugas untuk menyanyikan lagu Indonesia Raya dan Mengheningkan
Cipta. Rogu, berada pada baris pertama yang bertugas untuk memainkan
pianika. Setiap baris terdiri dari 5 orang anak. Dapatkah kamu
menghitung berapa jumlah seluruh anak yang bergabung dalam grup paduan
suara tersebut?
Squad, untuk menghitung jumlah seluruh anak dalam grup tersebut, kamu dapat menggunakan cara perkalian sebagai berikut:
5 x 5
Ternyata, perkalian di atas termasuk salah satu contoh dari perkalian berulang, lho. Kenapa? Karena perkalian tersebut terdiri dari bilangan dengan faktor-faktor yang sama, yaitu 5. Tahukah kamu, setiap perkalian berulang dapat ditulis secara ringkas dengan menggunakan notasi bilangan berpangkat seperti di bawah ini:
5² (dibaca 5 pangkat 2)
Nah, Jadi jawabannya sudah pada tahu ya, yaitu 5² = 5 x 5 = 25 orang anak.Oke, agar kamu lebih paham lagi tentang notasi bilangan berpangkat, yuk perhatikan contoh berikut:
2 x 2 x 2 = 2³ (dibaca 2 pangkat 3)
3 x 3 x 3 x 3 = 34 (dibaca 3 pangkat 4)
a x a x a x ... x a = an (dibaca a pangkat n)
Jika kamu melihat contoh-contoh di atas, maka dapat kamu ketahui kalau perpangkatan adalah suatu bilangan yang dikalikan dengan dirinya sendiri sebanyak jumlah pangkatnya (n kali). Pada prinsipnya, ternyata rumus perpangkatan pada bentuk aljabar sama dengan perpangkatan pada bilangan bulat.
Selain itu, terdapat beberapa bentuk istimewa yang akan sering kamu temui dalam perpangkatan aljabar, yaitu:
Sekarang, yuk, coba kerjakan soal di bawah ini supaya kamu semakin paham!
Contoh I: 
Penyelesaian:


Penyelesaian:
Nah, untuk contoh yang satu ini, penyelesaiannya cukup rumit nih,
Squad. Jadi, simak baik-baik ya langkah-langkahnya. Oke, langkah
pertama yang bisa kamu lakukan untuk menyelesaikan soal di atas adalah
operasikan persamaan tersebut seperti biasa.

Kemudian, langkah keduanya adalah kita samakan variabelnya.

Berdasarkan persamaan (3), didapat nilai q = 4. Lalu, kita substitusikan nilai q ke persamaan (2) menjadi sebagai berikut:

Setelah kita substitusikan niai q ke
persamaan (2), didapat nilai p = 5. Selanjutnya, kita substitusikan
nilai p ke persamaan (1) menjadi sebagai berikut:

Bagaimana sampai di sini? Paham atau paham? Nah, bagi kamu yang masih kurang paham, jangan ragu untuk tuliskan pertanyaanmu di kolom komentar, ya.
Squad, berdasarkan penjabaran di atas,
sekarang kamu sudah tahu bagaimana cara menyelesaikan operasi
perpangkatan pada bentuk aljabar berpangkat dua, kan. Lalu,
bagaimana cara untuk menyelesaikan operasi perpangkatan pada bentuk
aljabar yang pangkatnya lebih dari dua? Jawabannya ada dua cara, nih. Penasaran bagaimana caranya? Kalau begitu, yuk langsung simak contohnya di bawah ini!

- Cara I dengan menggunakan pola segitiga pascal
Segitiga pascal (sumber:en.wikipedia.org)
Pada gambar di atas dapat kamu ketahui
bahwa, pola bilangan tersebut membentuk bangun segitiga yang selalu
diawali dan diakhiri dengan angka 1. Kemudian, bilangan-bilangan yang
selain angka 1 itu diperoleh dari jumlah dua buah bilangan yang terletak
di atasnya dan saling berdekatan. Pola segitiga pascal ini ternyata berhubungan dengan koefisien pada bentuk aljabar, lho. Coba kamu perhatikan gambar di bawah ini!
Ternyata, koefisien pada bentuk aljabar di atas sama dengan pola segitiga pascal nih, Squad. Selanjutnya, coba kamu perhatikan besar pangkat pada masing-masing variabelnya. Ternyata, semakin ke kanan, besar pangkat variabel a akan semakin kecil (an --> an-1 --> ... --> a0) dan besar pangkat variabel b akan semakin besar (b0 --> ... --> bn). Jadi, berdasarkan soal di atas dapat kita peroleh hasil sebagai berikut:

Paham ya Squad dengan cara segitiga pascal ini. Oke, kalau begitu kita lanjut ke cara yang kedua, ya.
- Cara II
Nah, bagi kamu yang malas menghafal pola segitiga pascal di atas, kamu bisa menggunakan cara yang satu ini, nih. Pada cara ini, kamu hanya tinggal menguraikan aljabar tersebut menjadi sebagai berikut:

Wah, lumayan panjang ya, Squad.
Mungkin, untuk menyelesaikan bentuk aljabar dengan pangkat 3 dan 4,
cara ini masih cukup efektif. Tapi, bagaimana dengan bentuk aljabar yang
pangkatnya 5, 6, 7, dan seterusnya? Jangan sampai waktu kamu habis
hanya untuk menyelesaikan bentuk aljabar yang seperti itu, ya.
Oleh karena itu, ada pentingnya juga nih
untuk selalu mengingat pola segitiga pascal yang telah kita pelajari
sebelumnya. Selain itu, dalam mengerjakan soal-soal aljabar ini juga
dibutuhkan ketelitian yang tinggi. Perhatikan selalu tanda (+) dan (-) nya karena kedua tanda itu akan berubah ketika kamu melakukan operasi perkalian dan pemangkatan.
So, bagaimana tanggapanmu
setelah membaca artikel ini, Squad? Mudah atau sulit? Perlu kita akui
kalau materi aljabar ini memang cukup rumit, ya. Oleh karena itu, kamu
juga perlu untuk memperbanyak latihan soal, nih. Nah, bagi kamu yang masih belum paham dengan materi ini dan ingin tanya-tanya lebih lanjut lagi, kamu bisa lho gabung dengan JAGO MATEMATIKA. Belajar jadi semakin asik karena kamu juga bisa berdiskusi dengan teman-teman di seluruh Indonesia!
15 Mei 2019
Operasi Hitung Bentuk Aljabar
Pada dasarnya operasi hitung pada suku aljabar tidak berbeda dengan operasi hitung pada bilangan bulat. Coba kalian perhatikan contoh-contoh di bawah ini, kemudian kalian ambil kesimpulan sendiri apakah terdapat perbedaan antara operasi hitung suku aljabar dengan operasi hitung bilangan bulat.Pada pembahasan ini kita akan sedikit mengulas tentang bentuk-bentuk operasi hitung pada bentuk aljabar.
1. Operasi Penjumlahan dan Pengurangan Bentuk Aljabar
Operasi hitung penjumlahan dan pengurangan suku aljabar dilakukan dengan cara menjumlahkan atau mengurangkan koefisien antara suku-suku yang sejenis. Perhatikan contoh berikut ini!Tentukan hasil penjumlahan dan pengurangan bentuk aljabar berikut ini!
a. 4x + y – 2x
b. 3a2b – 5ab – 2a2b
Penyelesaian:
a. 4x + y – 2x = 4x – 2x + y
= 2x + y
b. 3a2b – 5ab – 2a2b = 3a2b – 2a2b – 5ab
= a2b – 5ab
Selain dengan cara di atas, penjumlahan dan pengurangan pada suku satu, suku dua, atau suku banyak dapat dihitung dengan cara bersusun ke bawah. Perhatikan contoh berikut ini!
Tentukan hasil penjumlahan dan pengurangan bentuk aljabar berikut ini!
a. 4x + 2x
b. 3a2b + 2ab2– 2a2b + 5ab2
c. 8x – 3x
d. 7ab2 – 3ab – 2ab2 – 8ab
Penyelesaian:
2. Operasi Perkalian dan Pembagian Bentuk Aljabar
Pada bentuk-bentuk aljabar berlaku sifat-sifat penjumlahan dan perkalian seperti pada bilangan bulat. Beberapa sifat tersebut antara lain:- Sifat komutatif penjumlahan, yaitu a + b = b + a
- Sifat asosiatif penjumlahan, yaitu a + (b + c) = (a + b) + c
- Sifat komutatif perkalian, yaitu a × b = b × a
- Sifat asosiatif perkalian, yaitu a × (b × c) = (a × b) × c
- Sifat distributif perkalian terhadap penjumlahan, yaitu: a × (b ± c) = (a × b) ± (a × c)
a. Perkalian Suku Satu dengan Suku Dua atau Suku Banyak
Berikut ini disajikan beberapa contoh perkalian suku satu, baik perkalian dengan suku dua atau dengan suku banyak.Tentukan hasil penjumlahan dan pengurangan bentuk aljabar berikut ini!
a. 4x (x – 2y)
b. 8a (3ab – 2ab2 – 8ab)
Penyelesaian:
Gunakan sifat distributif untuk menyelesaikan permasalahan di atas.
a. 4x (x – 2y) = (4x . x) – (4x (2y))
= 4x2 – 8xy
- = 8a ((3ab – 8ab) – 2ab2)
- = 8a ((-5ab) – 2ab
- = (8a x (-5ab)) – (8a . 2ab2)
- = -40a2b – 16a2b2 (bagi dengan –8)
- = 5a2b + 2a2b2
b. Perkalian Suku Dua dengan Suku Dua
Masih sama dengan perkalian sebelumnya, penyelesaian perkalian suku dua atau binomial tetap menggunakan konsep dasar sifat distributif.Misalkan kita mempunyai suku dua (binomial) yang berbentuk (a + b) dan (c + d). Langkah-langkah penyelesaian yang harus dilakukan adalah seperti terlihat pada gambar berikut.
Jadi (a + b)(c + d) = (ac + bc) + (ad + bd)
Perkalian suku dua dengan suku dua merupakan bentuk perkalian antara suku dua dengan dirinya sendiri atau dapat pula diartikan sebagai pengkuadratan suku dua. Misalkan kita mempunyai suku dua (x+y), maka langkah-langkah penyelesaiannya adalah sebagai berikut.
Coba kalian tentukan langkah-langkah penyelesaian untuk perkalian suku dua yang berbentuk (x-y)2!
Tentukan hasil kali dari (x + 2)2, kemudian sederhanakan!
Penyelesaian:
(x + 2)2 = (x + 2)(x + 2)
= x2 + 2x + 2x + 2 × 2
= x2 + 2(2x) + 4
= x2 + 4x + 4
Jadi (x + 2)2 = x2 + 4x + 4
c. Selisih Dua Kuadrat
Setelah kita mempelajari tentang perkalian suku dua dengan dirinya sendiri (bentuk kuadrat), sekarang kita akan membahas perkalian suku dua antara (x+y) dan (x-y).Langkah-langkah penyelesaiannya sama saja dengan penyelesaian bentuk (x + y)2 dan (x – y)2 yaitu:
Bentuk di atas dikenal dengan istilah selisih dua kuadrat. Agar lebih memahami tentang selisih dua kuadrat, pehatikan contoh berikut ini!
Tentukan hasil kali dari (x – 3)(x + 3)!
Penyelesaian:
(x – 3)(x + 3) = (x – 3)(x + 3)
= (x.x) + (x.3) + ((-3)x) + ((-3)(3))
= x2 + (3x) –3x – 9
= x2 – 9
Jadi (x – 3)(x + 3) = x2 – 9
Langganan:
Postingan (Atom)